A Nagy Bumm elmelet kerdojelei.

[Kukac]

Látod Rigel, ennél szebb kontrát nem is kaphattál volna!

Akkor írok neked majd mindig kozmológiai kérdéseket, és azt itt fejtegetjük.

Az első:

Sosem értettem, hogy lehet egységesen kezelni a csillagászati objektumok vöröseltolódását. Most nem arra gondolok, hogy milyen a csillagközi por hatása, vagy hogy ha egy galaxisban nincs Sn a1 robbanás, akkor nem tudjuk a távolságát.

Arra gondolok, hogy a minél messzebbről érkezik valaminek a fénye hozzánk, akkor az ugye, annál régebben indult el. Tehát az, amit most látunk, az ( a példa kedvéért) 1 milliárd éve történt esemény.
Tehát homogénnek és izotrópnak látjuk az univerzumot, pedig minnél messzebbről érkezik a fény, annál
régebbi eseményeket látunk. Amit most érzékelünk, már rég nem ott van, és nem az történik vele, amit éppen érzékelünk. Kötöttségeink miatt nem láthatunk ebben a pillanatban tőlünk nagyon távol,
de jelen pillanatban történő dolgokat, valamint nem láthatunk nagyon régen történt és hozzánk közel lévő dolgokat.

Nem okoz ez némi fejtörést a kozmológusoknak?

[Rigel]

Tehát homogénnek és izotrópnak látjuk az univerzumot, pedig minnél messzebbről érkezik a fény, annál régebbi eseményeket látunk.

Homogénnek és izotrópnak FELTÉTELEZZÜK az univerzumot (legalábbis megfelelő skálán vizsgálva), de nem annak LÁTJUK. Éppen amiatt, mert a fény véges sebességgel halad a rendszerben és senki "idebent" nem láthatja át egyidőben az egészet. Például kvazárok tekintetében egyáltalán nem látszik homogénnek az univerzum: a messze távolban hemzsegnek, itt a közvetlen szomszédságban viszont egy darab sincs belőlük.

Amit most érzékelünk, már rég nem ott van, és nem az történik vele, amit éppen érzékelünk.

Erről mindig ezek az galaxiseloszlás "térképek" jutnak az eszembe:

Ha jól megfigyeljük, akkor azt vesszük észre rajta, hogy valami rejtélyes oknál fogva tőlünk távolodva egyre lazább a galaxisok eloszlása. Míg a közvetlen környezetünkben jól lehatárolt galaxishalmazokba tömörülnek, a messzeségben valamiért diffúzabban helyezkednek el, és nemcsak azért, mert onnan kevesebb adat áll a rendelkezésre.
A rejtély megoldása persze az, hogy hiába számolták át a galaxistávolságokat a mai állapotra, a rajzon továbbra is megmarad az a "történetiség", amit a véges fénysebesség okoz egy ekkora rendszer megfigyelésekor. A térkép készítői rendelkeztek egy galaxisadattal, amire rászámolták a fényút időszükségletéből adódó plusz távolodást, de nem rendelkeztek azzal az információval, hogy a szóban forgó idő alatt a galaxis a lokális gravitációs centrumok felé mennyit mozgott. Így pedig a távoli galaxisokat kénytelenek voltak felrakni a térképre annak a diffúz elhelyezkedésnek az extrapolációjával, amiben akkoriban a galaxisok elhelyezkedtek.
Ha ránézek a térképre, mindig eszembe jut, hogy a széleken a diffúz eloszlás azóta biztosan pont ugyanolyan határozott szálakba rendeződött, mint a térkép közepén, ami a közelmúltat mutatja.

Kötöttségeink miatt nem láthatunk ebben a pillanatban tőlünk nagyon távol, de jelen pillanatban történő dolgokat, valamint nem láthatunk nagyon régen történt és hozzánk közel lévő dolgokat.

Nem okoz ez némi fejtörést a kozmológusoknak?

Azt nem tudom, de én gyakran terápiás kondicionálást csinálok éppen ennek a tudatosítására. Emlékeztetem magamat, hogy például a Tejútrendszer, meg az Andromeda galaxis is egykoron pont olyan kvazárok lehettek, mint amiket a messze távolban látunk. Amikor az első csillagok kigyulladtak, akkor itt nálunk is kék óriáscsillagok lobbantak ki néhány százmillió év alatt, azaz minden ugyanúgy történt itt is, mint ahogyan ott messze még mindig látjuk történni.
Ilyen szempontból szerencsésnek mondhatjuk magunkat. Ha feltételezzük, hogy a fizika ugyanaz mindenhol az univerzumban, akkor az itteni régmúltbeli történésekkel azonosakat megláthatjuk a "élő egyenes adásban" a messzeségben. És persze nyugodt szívvel feltételezhetjük, hogy éppen ebben a pillanatban (a Nagy Bummhoz képest definiálható az egyidejűség!) azokon a galaxisokon, amiket nem láthatunk, pont ugyanolyan viszonyok vannak, mint most itt nálunk.

[Sárki]

Na várj már, a kvazárok sugároznak, akkor a galaxisok közötti térben megbúvó fekete lyukaknak is sugározniuk kellett volna nem? Persze a te fekete lyukaid nyilván nem tettek ilyet, hiszen azok speciális tuarego-fekete lyukak amik komplett galaxisokat esznek és közben semmilyen sugárzás nem történik.
Egyáltalán tudod mennyi idő, mire kialakul egy fekete lyuk? Tisztában vagy azzal, hogy a kvazárok galaxisokban vannak? Tudsz róla, hogy a Tejútrendszer közepén is van egy szupermasszív fekete lyuk, mégis itt vagyunk?
Ismered egyáltalán a feltételeit, hogy mi kell egy fekete lyuk keletkezéséhez? Ha valamihez nem értesz, akkor ne akard már a komplett tudományágat megreformálni, úgy se sikerül. Pláne hogy a legalapvetőbb dolgokkal sem vagy tisztában.

[Dlajos]

off-
Kedves Kukac, Sanyilaci, Sárki!
Ne vegyétek el Tuarego kedvét a vitatkozástól, sőt legyetek ti is hálásak neki, mint én!
Ugyanis olyan válaszokat kap, főleg Rigeltől, olyan linkeket találtatok osztottatok meg miatta velünk is, érthető, jól felfogható példákat amik olvasása számomra nagy élmény. Mind ezt azonnali frissítésekkel!
Tuarego pedig kulturált formában erőlködik, ne bántsátok...
Üdv,
L.
on-
Hajime!

[Rigel]

Vagy visszaveszel az arcodból, és elfogadod, amit Rigel meg a többiek írtak, vagy mész a Nők Lapjára horoszkópot gyártani.

Azt azért tisztázzuk: én nem várom el senkitől, hogy elfogadja azt, amit írok. Nem vagyok szakértő a témában, maximum csak egy kicsit olvasottabb. Az én szavam itt nem számít, éppen ezért hozok mindig forrást is. Pusztán csak azt szeretném, ha a "vitapartner" utánanézne a dolgoknak az idézett vagy belinkelt forrásokban, alaposan elgondolkodna az (esetleg számára teljesen új) információn, és ha szükséges akkor ezek után módosítaná az elképzelését a dolgok működéséről.

[tobe_]

Vitázzatok csak, legalább van mit olvasni.

[Rigel]

Mivel ekkor még sűrű volt az anyageloszlás, így bőven volt anyagutánpótlása ennek az összehúzódásnak, így viszonylag hamar hatalmas anyagtömegek álltak össze és egyre sűrűbb, egyre forróbb testekké váltak. Első lépésben természetesen beindult a csillagképződés, majd hatalmas tömegüknél fogva szupernóvaként fel is robbantak. Maradványként azonban keletkezett egy fekete lyuk is, ami viszont tovább nyelte be az ekkor még mindig sűrű eloszlásban található anyagot. Az akkori körülmények miatt olyan nagy volt az anyagbeáramlás, hogy ennek mellékhatásaként irdatlan nagyságú felfénylések, energia-kisugárzások keletkeztek. Ezek lehettek, amit ma kvazárokként ismerünk.

Végül aztán, ahogy az Univerzum tágult és ritkult, úgy fogyott lassan el e gigantikus fekete lyukak körül a bekebelezhető anyag, s ettől fogva ott "csücsülnek" s "éheznek" a galaxisközi térben észrevehetetlenül.

Hát nem teszik.
Amikről te itt ilyen remek mesét költöttél, azok a mai napig népes sokasággal körbevéve bandáznak. "Galaxisoknak" nevezzük ezeket közönségesen.

Mert ugyanis ha volt ott "normál" anyag, ahol a feltételezett fekete lyukaid szerinted képződtek, akkor azok nem nyelhették el az összes anyagot. Valaminek még maradnia kell körülöttük gázfelhőként. (Aminek valami okból volt tangenciális irányú sebessége, az bizony jóval hosszabb spirális pályán zuhan bele a központi fekete lyukba!)
A fekete lyuk körüli gázfelhőben pedig sűrűséghullámok csillagokat hoznak létre, és máris előttünk áll a "korai anyagösszezuhanás" máig fejlődött képviselője: a galaxis.

Ja, és definíció szerint a galaxisközti térben nincsen galaxis.

[Rigel]

Ha valaki megmondja, hogy tudok itt írni felső indexeket, azt is megköszönöm.

Sehogy.
Rakd valami elérhető helyre a "Karaktertáblá"-t, és ilyen felső-index szükség esetén abból illeszd be a ² és ³ jeleket. Ennél magasabb hatványt, pláne képletet a hatványkitevőbe, viszont sehogy sem tudsz ilyen fórumokon beírni.

[Rigel]

Mit fejez ki az alábbi összefüggés?:
ds^2=a(t)^2ds3^2-c^2dt^2

Ez az ívelemnégyzet képlete az univerzum táguló téridejében.
Az gondolom már meg van, hogy általános esetben egy távolság valamilyen metrikával rendelkező ponthalmazban

alakban írható fel. Ez a Pithagorasz-tétel általánosítása, az ívelemnégyzet. A különböző koordinátakülönbségek páronkénti szorzataihoz tartozik egy-egy gij paraméter, amelyek a ponthalmaz dimenziószámának megfelelő darabszámú i és j indexelésűek. Ezekből a paraméterekből egy csinos kis mátrixot lehet összerakni, ahol az oszlopok mondjuk az i index szerint, a sorok meg a j index szerint vannak rendezve, a mátrix pedig az összes gij paramétert egybefoglalja. Ez a metrikus tenzor. Például egy sík kétdimenziós "euklideszi" tér esetén a metrikus tenzor főátlójában az értékek 1-esek, az összes többi helyen pedig nulla van. Ebből a fenti képlettel az jön ki, hogy
ds² = 1*dx² + 0*dx*dy + 0*dy*dx + 1*dy² = dx² + dy²

Sokkal érdekesebb a nem-euklideszi geometriák metrikus tenzora, mert ott mindenféle értékek szerepelhetnek az adott ij indexelésű helyen, ebből meg az következik, hogy a ds² ívelemnégyzet képlete is sokkal több tagból áll.
És akkor itt visszatérhetünk arra, hogy egy homogén-izotróp tágulásban lévő téridőnek is van metrikus tenzora, szerencsére olyan, hogy a tér minden pontjában ugyanazok az értékek az igazak. Azért jó ez, mert általánosan az Einstein-féle téregyenlet tartalmazza a metrikus tenzort, de ez pontról pontra más lehet egy összevissza görbült térben. A homogén-izotróp univerzum viszont nincs összevissza görbülve, így pedig "egyszerű" a geometriája, ezt egyszerű metrikus tenzor írhatja le.
A probléma itt az, hogy az univerzum metrikus tenzora függ az időtől! Az általad hozott ívelemnégyzet a descartesi koordinátarendszerben van felírva. Sajnos gyakrabban található meg a neten a polárkoordinátákkal felírt összefüggés:

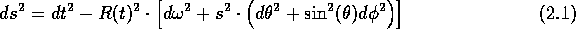
ami ezt a metrikus tenzort használja:

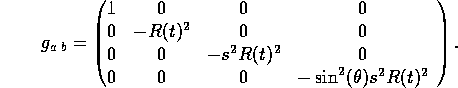
(Állandó a kavarás, hogy R(t) vagy a(t) használt, amit idemásoltam képet, abban valahol a c-t elrekkentették, hogy az idő- vagy a tér-elemekhez tartozó paraméterek a negatívak, de ettől függetlenül ugyanarról van szó.)
A tenzor bal felső eleme tartozik a dt²-hez, a maradék 3×3-as tenzorrész pedig egy táguló tér metrikus tenzora, speciel polárkoordinátarendszerben. A descartesi felírás annyiban különbözik ettől, hogy ugyanígy a metrikus tenzor főátlójában vannak nemnulla értékek, a bal felső szám -1 (vagy -c², ha nem rekkentik el) a maradék három nemnulla elem pedig a(t)². Ez jelzi, hogy a rendszer térszerű metszeteiben a távolságok függenek az időtől. Tágul. Amikor egy ilyen metrikus tenzorból összerakjuk az ívelemnégyzet képletét, akkor azt kapjuk, hogy lesz benne egy -c²dt² meg a térbeli távolságokból egy a(t)²ds3² tag:

A képletben feltűnő a(t) azt jelenti, hogy egy olyan rendszerről van szó, amelyben a térbeli távolságok változnak az idővel, esetünkben az a(t) skálaparaméter-függvény szerint.

[dgy]

Sanyilaci kérdezte:

Kezdjük a legelsővel, sztem könnyen tudtok rá válaszolni, nekem meg sok zsákutcát kellene végigjárnom.
Mit fejez ki az alábbi összefüggés?

A fenti alak egy próbafüggvény. Ilyen egyszerűsített alakban keressük az Univerzum "ívelemnégyzetét".

Kicsit részletesebben: a téridő két TETSZŐLEGES, infinitézimálisan közeli pontja ("események") közti ívelemnégyzet írható le:

ds^2=g_(kl) dx^k dx^l

alakban, a k és az l indexekre automatikusan összegezni kell 0-tól 3-ig. A metrikus tenzor g_(kl) komponensei (összesen 10 független adat, mert a tenzor szimmetrikus) a négy x^k koordináta TETSZŐLEGES függvényei lehetnek (persze folytonos, diffható stb függvények, ezt mindig feltesszük).

Az általános relativitáselmélet Einstein-egyenletei korlátozzák ezt a rengeteg lehetőséget: nem engedik meg tetszőleges g_(kl)(x) függvények fellépését, csak olyanokét, amelyek kielégítik az Einstein-egyenleteket. Ezek összekapcsolják a metrikus tenzor és inverze komponenseit, ezek hely és idő szerinti első és második parciális differenciálhányadosait az anyag eloszlására jellemző mennyiségekkel (ezeket az energiaimpulzus-tenzor tíz komponense tartalmazza). Az Einstein-egyenletek tíz darab nemlineáris másodrendű parciális diffegyenletből álló diffegyenletrendszert alkotnak: ez Novobátzky megfogalmazásában "ijesztő analítikai probléma". Maga Einstein is azt gondolta, hogy az egyenletek egzakt megoldására nincs remény.

Ma mégis igen sok (kb negyven) egzakt megoldást ismerünk. Hogy lehet ez? Úgy, hogy a fizikusok korlátozták az általánosságot: speciális fizikai feltételeket (leginkább szimmetriafeltételeket) kötöttek ki, amelyek csökkentették a g_(kl) tenzor független komponenseinek számát, emellett az Einstein-egyenletek némelyike a szimmetria fennállása esetén 0=0 azonosságként teljesül. Ha szerencsénk van, a független változók száma is csökken. Pl. gömbszimmetria feltételezése esetén (polárkoordinátarendszerben dolgozva) a metrikus tenzor komponensei nem függnek a polárszögektől, csak az r sugárirányú paramétertől és a t időtől. Schwarzshild 1917-ben épp egy ilyen megoldást vizsgált, és megmutatta, hogy üres tér esetén (ekkor az Einstein-egyenletek jobb oldalán az anyag hatását képviselő mennyiségek értéke nulla) még az időfüggés is kiküszöbölhető. Így a tíz parciális diffegyenlet helyett két (2) közönséges diffegyenlet marad (független változó az r sugárkoordináta), amelyek (teljesen véletlenül) egzaktul, analitikusan megoldhatók. Így kapjuk a Schwarzschild-megoldást, amely alapvető fontosságú, hiszen ez írja le a gömbszimmetrikus csillag (avagy fekete lyuk) körüli üres teret - speciális alkalmazásként a bolygómozgást vagy a fénynek a csillag melletti eltérülését.

A kozmológiai megoldás során hasonló, de más szimmetriafeltételeket kell feltételeznünk.

1/ Létezik "világidő", azaz az egész téridő egyszerre, globálisan szinkronziálható (pontosabban: lehet olyan koordinátázást választani a négydimenziós sokaságban, amelyben ez a feltétel teljesül). Ebből következik, hogy a metrikus tenzor g_(01), g_(02) és g_(03) komponense azonosan nulla. Az ívelemnégyzetben tehát különválaszthatjuk a g_(00) együtthatójú dx^0*dx^0 mennyiséget (pongyolán: dt^2) és a három térbeli differenciálkomponens szorzataiból előálló "háromdimenziós" ívelemnégyzetet, amit egy előjelváltással "távolságnégyzetnek" is nevezhetünk. Tehát:

ds^2=g_(00) dt^2 – dl^2

ahol a térbeli ívelemnégyzet továbbra is egy összeg:

dl^2= - g_(kl) dx^k dx^l = G_(kl) dx^k dx^l

de az öszegezés most már csak 1-től 3-ig fut. A G_(kl) mennyiségek egy 3*3-as (pozitív definit) „térbeli” metrikus tenzort alkotnak, melynek komponensei természetesen függnek a vizsgált pont térbeli koordinátáitól – sőt (és ez nagyon fontos!) a negyedik koordinátától, az időtől is.

2/ A következő feltevésünk: a t világidő minden pontban megegyezik az ott „nyugvó” megfigyelő (pl galaxis) d tau sajátidejével. Ennek matematikai kifejezése: g_(00) = 1. Tehát az ívelemnégyzet tovább egyszerűsödik:

ds^2 = dt^2 – dl^2

A dl^2 térbeli ívelemnégyzet továbbra is dl^2= G_(kl) dx^k dx^l alakú, G_(kl) a hely és az idő függvénye.

3/ A harmadik szimmetriafeltevék a legerősebb: ezt hívják „kozmológiai elvnek”. Azt tesszük fel, hogy rögzített t időben a három térbeli koordinátától függetlenül a fizikai viszonyok mindenütt azonosak („a világ homogén”). Ez egyebek között az is jelenti, hogy a tér (nem a téridő!) tetszőleges pont körül gömbszimmetrikus, azaz a metrikus tenzor nem függ a polárszögektől (pontosabban a közönséges euklideszi geometriából ismert módon függ tőlük), csak a radiális r koordinátától (no meg persze az időtől). Kiderült, hogy a homogenitást matematikailag úgy lehet megfogalmazni, hogy kiszámítjuk a téridő háromdimenziós „most-felületeinek”, térszerű szeleteinek skalárgörbületét (ehhez a G_(kl) 3*3-as tenzor komponenseit, valamint ezek hely szerinti első és második deriváltjait kell felhasználnunk), majd megköveteljük, hogy ez a mennyiség mindenütt azonos legyen, azaz NE FÜGGJÖN a térbeli koordinátáktól. Ez két másodrendű egyenletet jelent a csak r-től (és t-től) függő G_(kl) tenzor r szerinti deriváltjaira. Ezek az egyenletek egzaktul megoldhatók. Az eredmény eléggé egyszerű alakba írható:

dl^2 = a^2 {dr^2 + S(r)^2 [d teta ^2 + (sin teta)^2 d fi^2]}

ahol teta és fi a szokásos polárszögek. A szögletes zárójelben felismerhetjük az egységgömb felületén mért távolság euklideszi kifejezését. Az „a” mennyiség egy pozitív állandó.

Az S(r) függvénynek is ki kell elégítenie egy közönséges differenciálegyenletet (megfelelő határfeltételekkel), ennek három lehetséges megoldása van:

S(r) = sin r, S(r) = r, S(r) = sh r

A konstans t időhöz tartozó „terek” a három esetnek megfelelően zárt (hipergömb), sík (euklideszi tér), illetve Bolyai-Lobacsevszkij-tér lehetnek. (Érdemes kiszámítani a három esetben az R sugarú körök kerületét: csak a középső, euklideszi esetben kapjuk az ismert 2 pi R értéket, a másik két esetben a „tér” geometriája nemeuklideszi.)

Ne felejtsük el, hogy a G_(kl) 3*3-as tenzor komponensei az r sugár mellett a t időnek is függvényei lehetnek. A sugárfüggést az S(r) függvénnyel már megadtuk. De hová bújt a legutóbbi képletből az időfüggés? Bingó: az „a” „állandó” még tetszőleges módon függhet az időtől!

Eredményünk tehát a következő: az 1/, 2/ és 3/ szimmetriafeltevések fennállása esetén az ívelemnégyzet (azaz a téridő két tetszőleges, ám infinitézimális közelségben levő pontja közti négydimenziós távolságnégyzet a következő alakba írható:

ds^2 = dt^2 - a(t)^2 {dr^2 + S(r)^2 [d teta ^2 + (sin teta)^2 d fi^2]}

E képletben (c=1 rendszerben) t a világidő, ami egyben a koordinátarendszerünkben nyugvó tömegpontok sajátideje, teta és fi egy tetszőleges térbeli pont körüli tetszőleges tengelyhez képesti polárszögek, r a tetszőleges térbeli origótól számított radiális koordináta , az a(t) függvény pedig tetszőleges.

Kielégítettük tehát a három szimmetriafeltételt. Az így kapott metrika a Robertson-Walker-metrika nevet viseli (bár már Fridman felírta, de a fenti szisztematikus levezetés RW-nek köszönhető).

Ha egy rögzített t időben kiszámítjuk két, egymástól véges (tehát nem infinitézimális) messzeségben levő, ám a koordinátarendszerünkhöz képest nyugvó tömegpont távolságát, akkor a dl térbeli ívhosszat kell kiintegrálnunk. Tegyük az egyik tömegpont helyére a (tetszőlegesen választható) origót, és mutasson a(z ugyancsak tetszőlegesen választható) polártengely a másik tömegpont felé. Ekkor a két pont közti vonalon csak az r koordináta változik, 0-tól mondjuk R-ig. A két pont távolsága:

L = Int (0, R) dl = a(t) Int (0, R) dr = a(t) R

A koordinátarendszerünkben rögzített, időben nem változó r koordinátájú (r=0 és r=R) két tömegpont L(t) távolsága tehát az a(t) „skálafüggvénnyel” arányosan változik. Ezt szoktuk az ismeretterjesztő irodalomban úgy megfogalmazni, hogy „nem a galaxisok mozognak, hanem a tér tágul közöttük”.

No de hol vannak az Einstein-egyenletek, hol az anyag téridő-görbítő hatása, egyáltalán: hol az anyag?

Még sehol! Ugyanis eddig nem használtuk fel a metrikus tenzort meghatározó Einstein-egyenleteket, ezért a teret kitöltő anyag semmiféle tulajdonságát sem! Ennek ellenére MAJDNEM meghatároztuk a metrikus tenzort, hiszen az ívelemnégyzet RW-alakjában (az S(r) függvény három lehetséges alakja közti választás után) már csak egyetlen ismeretlen, egyváltozós a(t) függvény maradt. Ezt az egyszerűsítést (tíz darab négyváltozós függvény helyett egyetlen egyváltozós függvény) a felhasznált szimmetriaelvek nagyon erős volta tette lehetővé.

Már csak ez a lépés van hátra: a metrikus tenzor (és deriváltjai) MAJDNEM pontosan meghatározott fenti alakját behelyettesítjük a gravitációt, azaz a metrikát meghatározó Einstein-egyenletekbe. Ennél a lépésnél kell feltevést tennünk a teret kitöltő anyag tulaldonságaira: az Einstein-egyenletek jobb oldalán ugyanis megjelenik az energiaimpulzus-tenzor – ami ilyen speciális szimmetria esetén csakis az energiasűrűséget és a hidrosztatikai nyomást tartalmazza (a kozmológiai elv szerint ezek a mennyiségek adott időpillanatban állandók, tehát csak az idő függvényei lehetnek). Mivel az a(t) függvényen kívül minden ismert, az Einstein-egyenletek tíz komponense az a(t) függvényre ad egyenleteket. Hálistennek egy csomó egyenlet azonosan teljesül, mások meg megegyeznak egymással. Marad KÉT közönséges diffegyenlet az a(t) függvényre – és persze az egyenletekben frissen felbukkant e(t) és p(t) függvényekre, ahol e az energiasűrűség, p pedig a nyomás.

Szükségünk van még egy egyenletre, ez pedig az állapotegyenlet lesz: az energiasűrűség és a nyomás közti lokális kapcsolatot leíró, a gravitációtól teljesen független, a termodinamikából, statisztikus fizikából vagy a kvantummező-elméletből levezethető összefüggés.

A három egyenlet együtt már meghatározza a három függvényt, így egyebek között az a(t) skálafüggvényt is, ami „az Univerzum tágulásának” kulcsmennyisége.

Ezzel a módszerrel (és a jelenlegi, „galaxisporral” kitöltött Univerzumra vonatkozó p=0 állapotegyelet feltételezésével) jutott Fridman 1921-ben az azóta sokat idézett három görbéhez (ami az S(r) függvény három lehetséges választásának felelt meg). Ő számításai során az eredeti, kozmológiai állandót nem tartalmazó Einstein-egyenleteket használta. Lemaitre a húszas években már figyelembe vette a lambda kozmológiai állandót is, így sok újfajta megoldást kapott (ugyanazon egyenlet két önkényes paraméterének különböző kombinációi esetén), egyebek között megkapta azt az először lassuló, majd egy inflexiós pont után gyorsulóba átváltó megoldást is, amit aztán a kilencvenes évek kozmológiai megfigyelései (majd az azóta folyó további kutatások) igazoltak, és paramétereit a mérési eredményeihez igazítottak.

Ezek a megoldások mind a p=0 állapotegyenlet feltételezésével születtek, tehát csak az Univerzum életének abban a szakaszában érvényesek, amikor nyomás nélküli „galaxispor” (emellett sötét anyag, no meg kvinteszencia – de hát ezek nyomása is nulla) tölti ki. Ez a korszak lefedi az utóbbi tizenvalahány milliárd évet, az első néhány százezer év kivételével. A korábbi korszakokban elektromágneses sugárzás, még korábban a leptonokból, illetve hadronokból álló „ősi tűzgömb”, azelőtt pedig a túlhűtött Higgs-vákuum, előtte meg a feltételezett kvantumhab töltötte ki a világot – az Einstein-egyenletekbe ezen anyagfajták energiasűrűségét és nyomását, illetve a köztük fennálló összefüggést leíró állapotegyenletet (ha majd sikerül ezeket felírni) kell behelyettesíteni. Így másfajta skálafüggvényeket, tágulási görbéket kapunk, ezeket a korszakhatárokon össze kell illeszteni, hogy eljussunk az Univerzum teljes történetét leíró a(t) függvényhez. És ha van valamilyen hipotézisünk a mi korszakunkat követő eónokban az Univerzumot majdan domináló anyag tulajdonságairól, akkor a Robertson-Walker-metrikát megtartva, de az állapotegyenletet kicserélve e távoli korokra is meghosszabbíthatjuk az a(t) skálafüggvény görbéjét – a Nagy Brrr, esetleg a Nagy Reccs vagy a Nagy Zitty irányába...

dgy